

Lab 3 (RDP)¶

En este laboratorio aprenderán a implementar un Recursive Descent Parser para una gramática simple.

1. Introducción¶

En las últimas clases ustedes vieron el tema de Recursive Descent Parsing (RDP para simplificar), aprendieron que es un tipo de parser predictivo y que entra en la categoría de top-down parsing. También vieron de forma general un algoritmo para implementarlo y en este laboratorio lo pondremos en práctica.

Como el nombre sugiere, un Recursive Descent Parser usa funciones recursivas para implementar un parser predictivo. La idea central es que cada no terminal en la gramática es representado por una de esas funciones recursivas. Cada función entonces mira el siguiente token (1 token de lookahead) para poder escoger así, una de las producciones de algún no-terminal. De esta manera es como vamos analizando la entrada y construyendo nuestro árbol (si es que la entrada tiene una sintáxis correcta, de lo contrario desplegaríamos algún error).

Recuerden que:

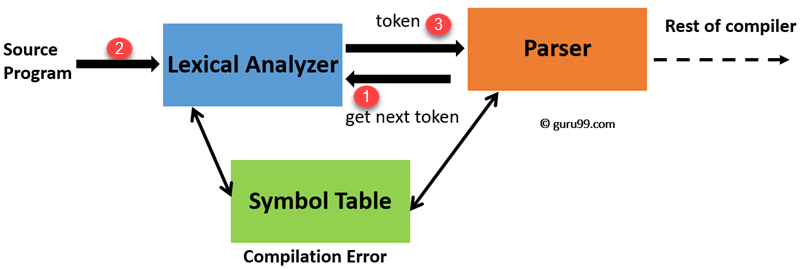
Un analizador léxico (lexer) convierte texto (raw-text) en un stream de tokens.
Un analizador sintáctico (parser) convierte el stream de tokens en un AST.

De forma gráfica esos 2 pasos los podemos ver asi:

En este laboratorio realizaremos una calculadora con un par de operaciones e iremos un paso más adelante al implementar un intérprete, es decir no crearemos un árbol sintáctico sino que evaluaremos en el momento las expresiones.

2. Gramática¶

La gramática con la que trabajaremos es la siguiente:

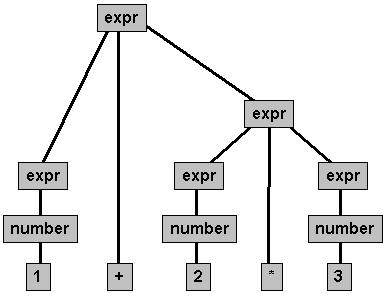
S ::= E;
E ::= E + E
  |   E - E
  |   E * E
  |   E / E
  |   E % E
  |   E ^ E
  |   - E
  |   (E)
  |   number

# number en nuestro caso significara un double

Esta gramática tiene un gran problema para nuestro RDP. Si se recuerdan por lo visto en clase, sufre de un problema llamado left-recursion. Una de las desventajas de este tipo de parsers es que las gramáticas con las que puede trabajar son aquellas que no son recursivas hacia la izquierda y claramente esta lo es, E ::= E + E por ejemplo. Así que lo que necesitamos hacer primero es transformar nuestra gramática para que no tenga este problema, teniendo en cuenta siempre que el lenguaje que describe nuestra nueva gramatica G1 es el mismo que describe nuestra gramática G original, es decir:

$$L(G1) = L(G)$$

3. Lexer¶

Para el primer ejercicio de este laboratorio, ustedes van a implementar el lexer para la gramática de nuestra calculadora utilizando JLex. El motivo principal de esto es para que sigan ganando práctica con esta herramienta, que surgan dudas y que los ayude a empezar/avanzar con el proyecto.

Para empezar clonen el siguiente repositorio de Github Classroom:

https://classroom.github.com/a/EsfgDA-Z

Dentro del repositorio van a encontrar un archivo llamado lexer.lex, en ese archivo ustedes tienen que definir el lexer para la gramática. Dentro de ese archivo hay en forma de comentarios algunas instrucciones para guiarlos.

3.1 Clase Token¶

En el directorio de trabajo hay una clase llamada Token que nos va a servir para representar los tokens de la gramática y es el tipo de objeto que tenemos que devolver dentro de las acciones del lexer. Esta clase tiene 2 constructores:

Token(int id, String val)
Token(int id)

Dentro de esta clase también están definidos los IDs que representan cada token y tienen que hacer uso de ellos cuando encuentren un token. En ese archivo también están definidos otros métodos que pueden ser útiles para la siguiente parte del laboratorio.

Ejemplo:

// Asi se veria en la parte de acciones del archivo .lex
<YYINITIAL>{SEMI}   { return new Token(Token.SEMI);             }
<YYINITIAL>{NUMBER} { return new Token(Token.NUMBER, yytext()); }

Cuando tengan listo más de algo, pueden probar lo que hicieron utilizando el siguiente comando:

make lexer
./lexer "2 + 2;"
NUMBER : 2
+
NUMBER : 2
;

Aviso: En ocasiones el símbolo * puede dar problema al probar esta parte del lab. No se preocupe mucho por esto y siga trabajando las demás partes.

4. Parser¶

Para el segundo ejercicio de este laboratorio ustedes implementarán un RDP. Esta gramática es bastante simple y prácticamente se trata solo de expresiones aritméticas. Parsear expresiones de este tipo con recursive descent tiene 2 problemas:

Obtener un árbol sintáctico que siga la precedencia y la asociatividad de los operadores.
Hacerlo eficientemente cuando hay muchos niveles de precedencia.

En clase ustedes vieron la clásica solución para el primer problema, que a pesar de que es bastante buena y elegante, no resuelve el segundo problema. En este laboratorio les vamos a enseñar una técnica llamada Shunting Yard Algorithm que es más eficiente y resuelve los dos problemas, la base de este algoritmo se encuentra hasta en las calculadoras chicleras.

4.1 Clase Parser¶

En el directorio de trabajo van a encontrar un archivo llamado Parser.java, en este archivo es donde ustedes tienen que implementar el parser. Prácticamente lo que tienen que hacer es crear una plantilla con funciones recursivas de la gramatica que modificamos. Aquí hay unas funciones que les pueden ser útiles como term().

Ejemplo:

Si nuestra gramática empieza de esta manera S ::= E; podriamos implementarlo de la siguiente manera.

boolean S() {
    return E() && term(Token.SEMI);
}

boolean E() {
    ...
}

4.2 Shunting Yard Algorithm¶

La idea del algoritmo Shunting Yard es mantener los operadores en un stack hasta que todos los operandos han sido parseados. Los operandos se mantienen en un segundo stack. El algoritmo shunting yard puede utilizarse directamente para evaluar las expresiones mientras son parseadas (como un interprete, que es lo que vamos hacer).

La idea central del algoritmo es mantener los operadores en el stack ordenados por precedencia (la precedencia más baja en el fondo del stack y la más alta en el top del stack), por lo menos en la ausencia de paréntesis. Antes de meter un operador en el stack de operadores, todos los operadores que tienen mayor precedencia son sacados del stack. Sacar un operador del stack de operadores consiste en remover el operador y sus operandos del stack de operandos, evaluar, y meter el resultado en el stack de operandos. Al final de una expresión los operadores que quedan son sacados y evaluados con sus respectivos operandos.

La siguiente tabla ilustra el proceso para un input : x * y + z. El stack se va llenando a la izquierda.

push(a) : hace push de a en el stack de operandos
pushOp(op) : hace push de un operador en el stack de operadores
pre(op) : devuelve precedencia de un operador

4.3 Precedencia¶

Para nuestra gramática la precedencia es la siguiente de mayor a menor:

( )
- unario
^
* / %
+ -

Dentro del archivo que tienen que modificar, ustedes tienen que llenar con código donde hay comentarios que dicen /*TODO CODIGO AQUI*/.

Para probar su RDP tienen que hacer lo siguiente:

make parser
./parser
>>> 2 + 2;
4.0
>>>

Entrega¶

Recuerde hacer add + commit + push y subir el link de su repositorio al GES.